🧮 Math#

#bs.math:help

The beatifull world of mathematics… in Minecraft!

$../_images/math-light.png$ $../_images/math-dark.png$

“Mathematics has very subtle inventions that can be of great service, both to satisfy the curious and to facilitate all arts and reduce the labor of men.”

—René Descartes

Watch a demo

🔧 Functions#

You can find below all functions available in this module.

Combine#

#bs.math:combine

Compute the combine of 2 numbers.

Inputs:: Scores $math.combine.[m,n] bs.in: Numbers to be combined, the smaller input will be taken from the greater input.
Outputs:: Return | Score $math.combine bs.out: Result of the operation.

Technical limitation

The value of bs.out is incorrect if the result is greater than 2147483647 or $math.combine.[m,n] bs.in are not both positive.

Compute $combine(4,2)$:

# Once
scoreboard players set $math.combine.m bs.in 4
scoreboard players set $math.combine.n bs.in 2
function #bs.math:combine
tellraw @a [{"text": "combine(4,2) = ","color":"dark_gray"},{"score":{"name":"$math.combine","objective":"bs.out"},"color":"gold"}]

Credits: Ethanout

Exponential#

#bs.math:exp

Compute the exponential function.

Inputs:: Storage bs:in math.exp.value [number]: Number to be exponentiated.
Outputs:: Storage bs:out math.exp [double]: Result of the operation.

Technical limitation

Due to the limit of integers that can be stored in a score, the interval of bs:in is limited to [-6,15[.

Compute $exp(3)$:

# Once
data modify storage bs:in math.exp.value set value 3.0
function #bs.math:exp
data get storage bs:out math.exp

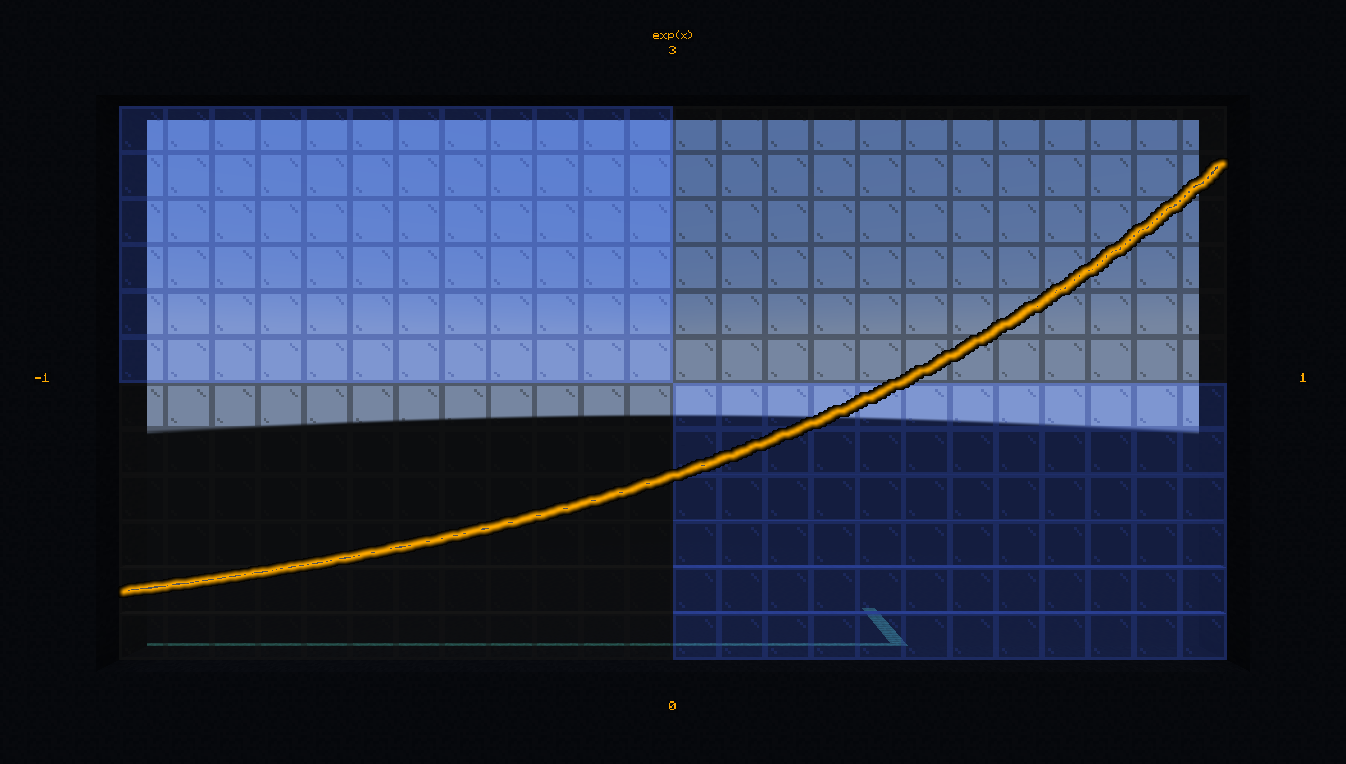
Credits: Aksiome, KubbyDev

Factorial#

#bs.math:factorial

Compute the factorial of the number.

Inputs:: Score $math.factorial.n bs.in: Number to be factorialized.
Outputs:: Return | Score $math.factorial bs.out: Result of the operation.

Technical limitation

Due to the limit of integers that can be stored in a score, the interval of bs.in.0 is limited to [0,12].

Compute $3!$:

# Once
scoreboard players set $math.factorial.n bs.in 3
function #bs.math:factorial
tellraw @a [{"text": "3! = ","color":"dark_gray"},{"score":{"name":"$math.factorial","objective":"bs.out"},"color":"gold"}]

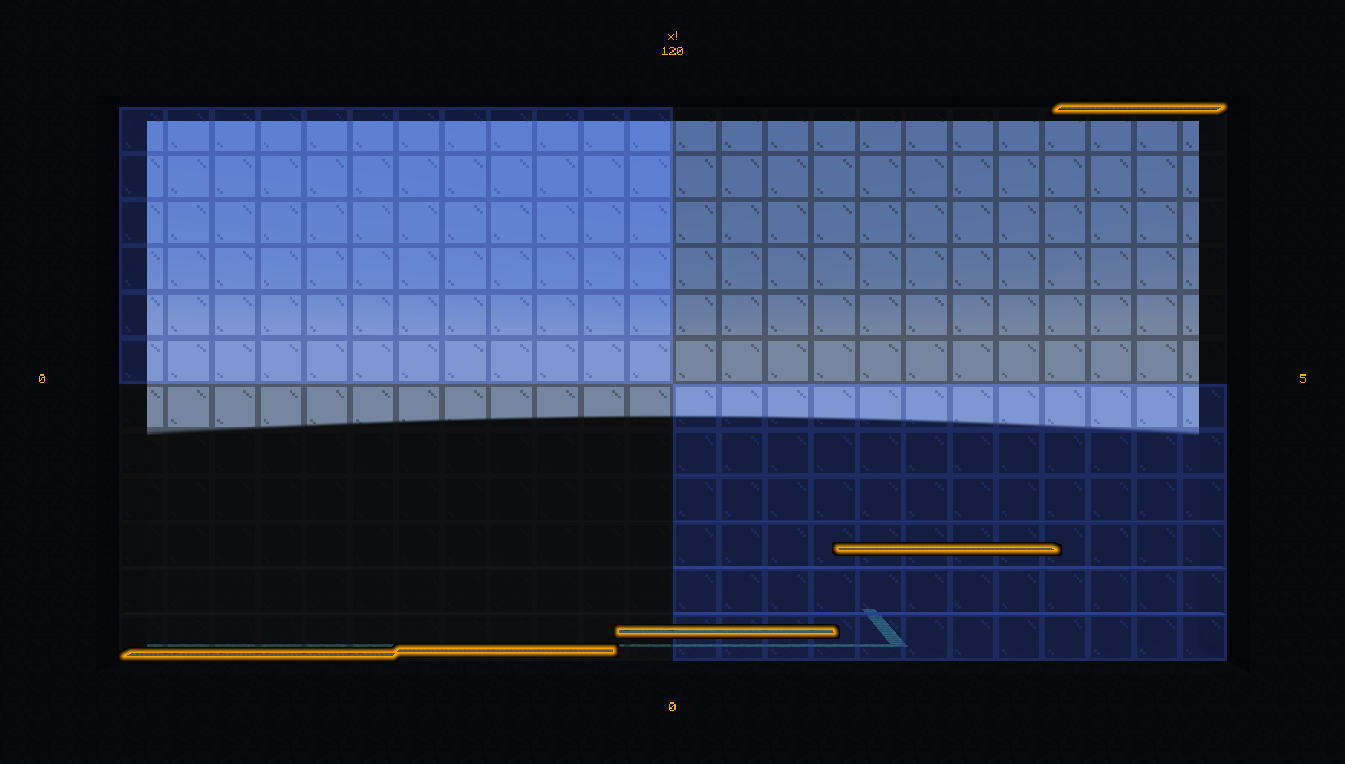
Credits: KubbyDev

Float radix#

#bs.math:frexp

Decompose a floating point number into a normalized fraction and an integral power of two.

Inputs:

Storage bs:in math.frexp.value [number]: Number to be decomposed.

Outputs:

Storage bs:out math.frexp.e [int]: Exponent for the power of 2.

Storage bs:out math.frexp.x [double]: Normalized fraction in range ]-1,-0.5] or [0.5,1[.

Decompose 5.8 into its mantissa and exponent:

# Once
data modify storage bs:in math.frexp.value set value 5.8
function #bs.math:frexp
data get storage bs:out math.frexp

Credits: Aksiome

Greatest common denominator#

#bs.math:gcd

Compute the greatest common denominator of two numbers.

Inputs:: Scores $math.gcd.[a,b] bs.in: The two numbers.
Outputs:: Return | Score $math.gcd bs.out: The greatest common denominator.

Calculate the greatest common denominator between 16 and 12:

# Once
scoreboard players set $math.gcd.a bs.in 16
scoreboard players set $math.gcd.b bs.in 12
function #bs.math:gcd
tellraw @a [{"text": "gcd(16,12) = ", "color": "dark_gray"},{"score":{"name":"$math.gcd", "objective": "bs.out"}, "color": "gold"}]

Credits: Aksiome, Leirof

Inverse trigonometry#

Acos

#bs.math:acos

Compute the arc cosine of a value between -1 and 1.

Inputs:: Score $math.acos.value bs.in: Value you want to compute the arccosine of, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores.
Outputs:: Return | Score $math.acos bs.out: Result of the operation in degrees, shifted by 2 digits.

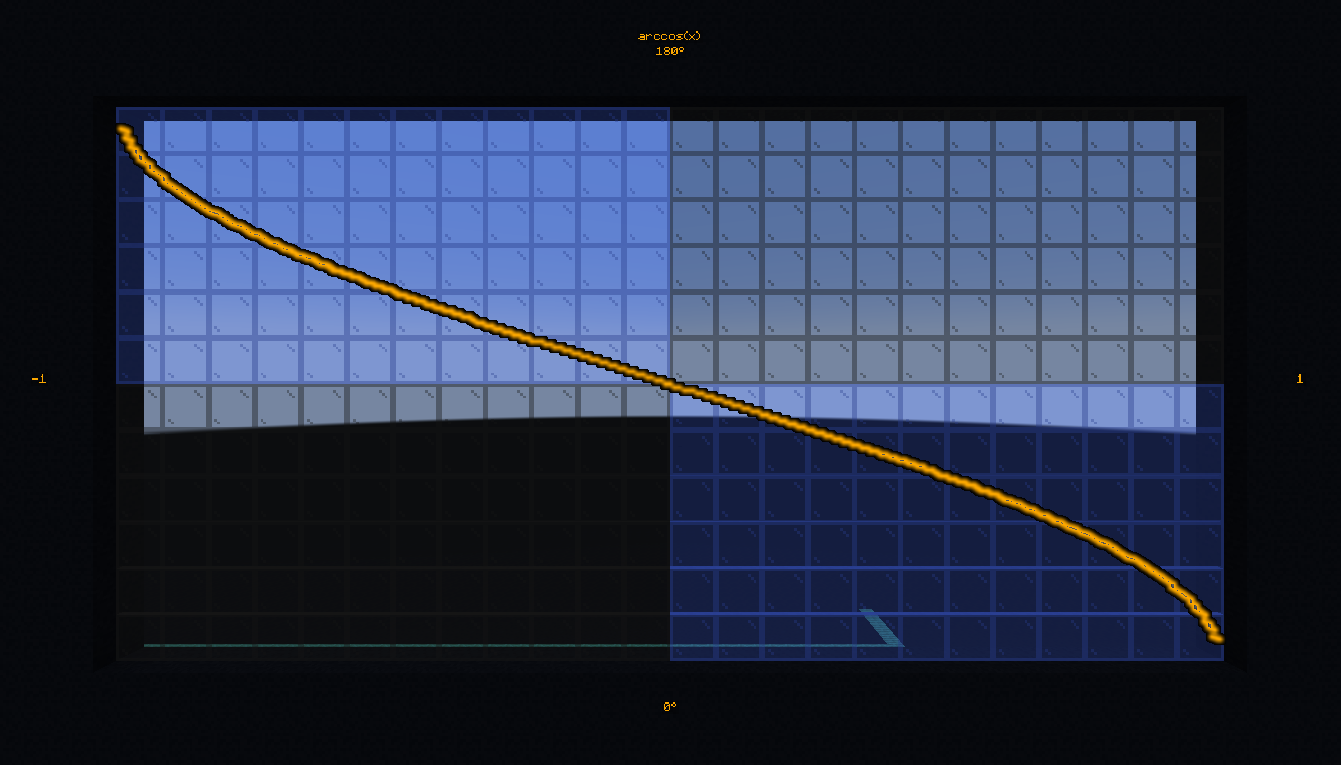
Compute and display the arccosine of 0.42:

# Once
scoreboard players set $math.acos.value bs.in 420
function #bs.math:acos
tellraw @a [{"text":"acos(0.42) = ","color":"dark_gray"},{"score":{"name":"$math.acos","objective":"bs.out"},"color":"gold"}]

Asin

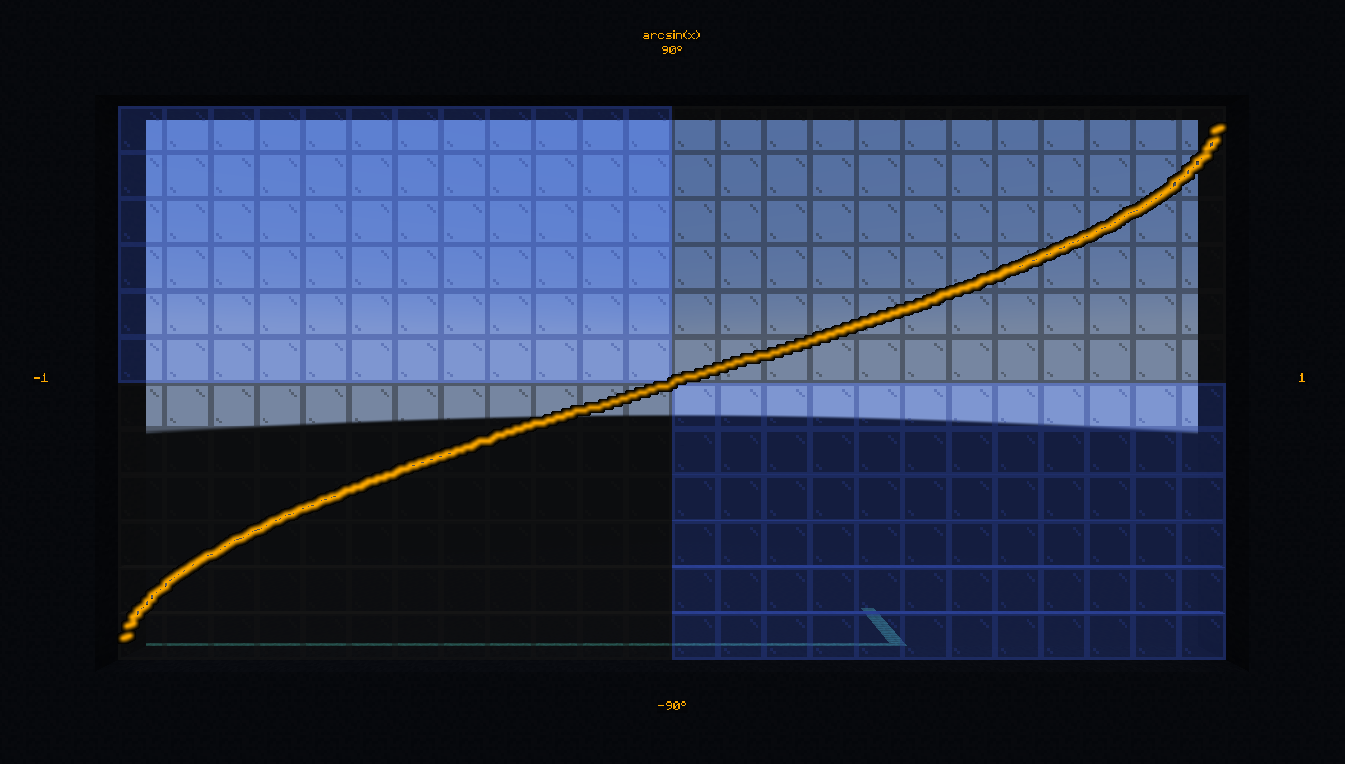
#bs.math:asin

Compute the arc sine of a value between -1 and 1.

Inputs:: Score $math.asin.value bs.in: Value you want to compute the arcsine of, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores.
Outputs:: Return | Score $math.asin bs.out: Result of the operation in degrees, shifted by 2 digits.

Compute and display the arcsine of 0.42:

# Once
scoreboard players set $math.asin.value bs.in 420
function #bs.math:asin
tellraw @a [{"text":"asin(0.42) = ","color":"dark_gray"},{"score":{"name":"$math.asin","objective":"bs.out"},"color":"gold"}]

Atan

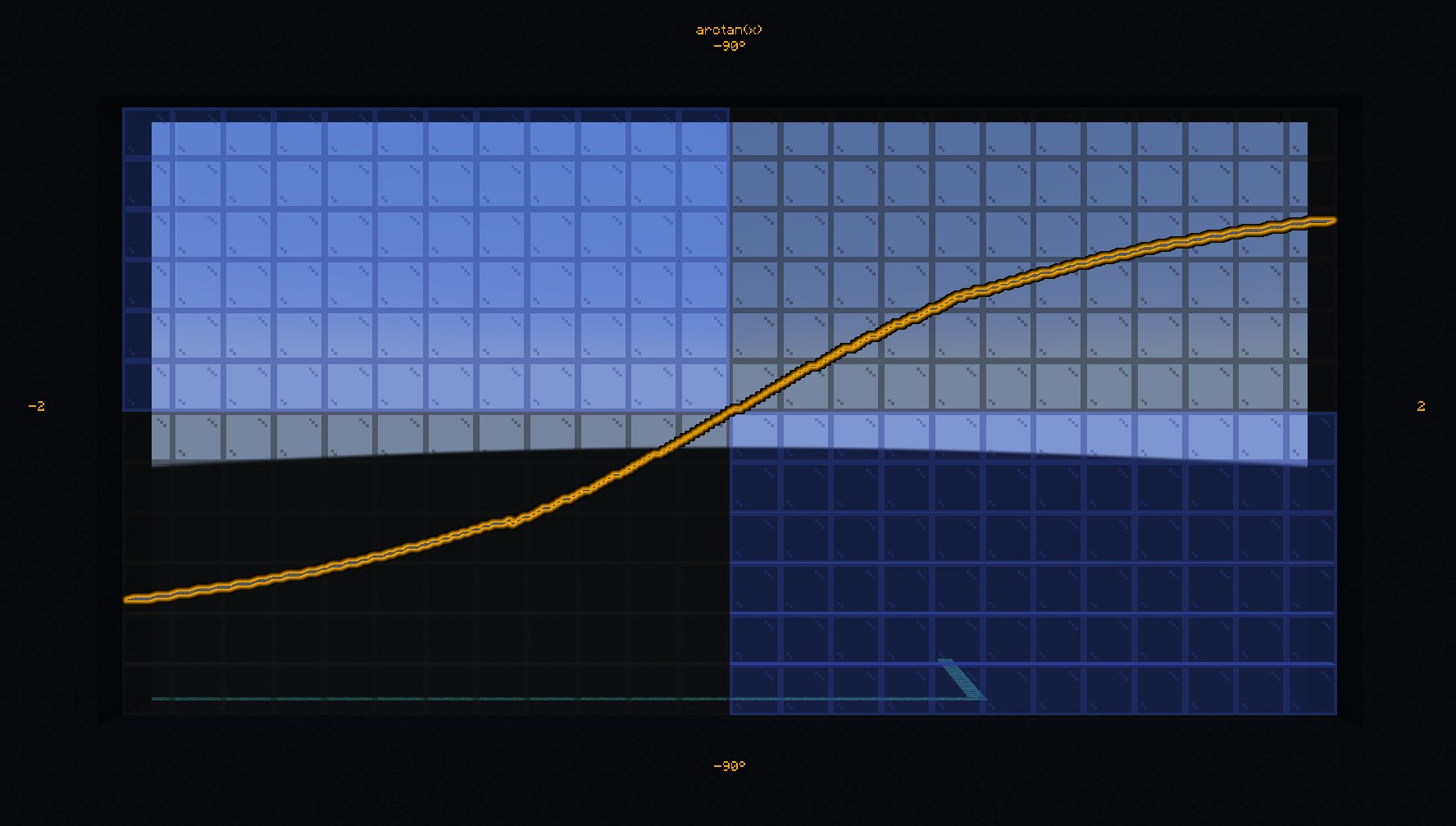
#bs.math:atan

Compute the arc tangent of a value between -infinite and +infinite.

Inputs:: Score $math.atan.value bs.in: Value you want to compute the arctangent of, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores.
Outputs:: Return | Score $math.atan bs.out: Result of the operation in degrees, shifted by 2 digits.

Compute and display the arctan of 0.42:

# Once
scoreboard players set $math.atan.value bs.in 420
function #bs.math:atan
tellraw @a [{"text":"atan(0.42) = ","color":"dark_gray"},{"score":{"name":"$math.atan","objective":"bs.out"},"color":"gold"}]

Atan2

#bs.math:atan2

Compute the 2-argument arctangent of y and x.

Inputs:: Scores $math.atan2.[y,x] bs.in: Values you want to compute the arctangent of, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores.
Outputs:: Return | Score $math.atan2 bs.out: Result of the operation in degrees, shifted by 2 digits.

Compute and display the atan2 of (0.42, 0.8):

# Once
scoreboard players set $math.atan2.y bs.in 420
scoreboard players set $math.atan2.x bs.in 800
function #bs.math:atan2
tellraw @a [{"text":"atan2(0.42, 0.8) = ","color":"dark_gray"},{"score":{"name":"$math.atan2","objective":"bs.out"},"color":"gold"}]

Credits: Aksiome, KubbyDev, Leirof

Logarithm#

Base e (Neperian)

#bs.math:log

Compute the Neperian logarithm (base e) of a number.

Inputs:: Storage bs:in math.log.value [number]: Number to be logarithmized.
Outputs:: Storage bs:out math.log [double]: Result of the operation.

Calculate $ln(28)$:

# Once
data modify storage bs:in math.log.value set value 28.0
function #bs.math:log
data get storage bs:out math.log

Base 2

#bs.math:log2

Compute the logarithm in base 2 of a number.

Inputs:: Storage bs:in math.log2.value [number]: Number to be logarithmized.
Outputs:: Storage bs:out math.log2 [double]: Result of the operation.

Calculate $log_2(28)$:

# Once
data modify storage bs:in math.log2.value set value 28.0
function #bs.math:log2
data get storage bs:out math.log2

Base 10

#bs.math:log10

Compute the logarithm in base 10 of a number.

Inputs:: Storage bs:in math.log10.value [number]: Number to be logarithmized.
Outputs:: Storage bs:out math.log10 [double]: Result of the operation.

Calculate $log_{10}(28)$:

# Once
data modify storage bs:in math.log10.value set value 28.0
function #bs.math:log10
data get storage bs:out math.log10

Base a

#bs.math:loga

Compute the logarithm in base a of a number.

Inputs:

Storage bs:in math.loga.value [number]: Number to be logarithmized.

Storage bs:in math.loga.a [number]: Base of the logarithm.

Outputs:

Storage bs:out math.loga [double]: Result of the operation.

Calculate $log_4(28)$:

# Once
data modify storage bs:in math.loga.a set value 4
data modify storage bs:in math.loga.value set value 28.0
function #bs.math:loga
data get storage bs:out math.loga

Credits: Aksiome, KubbyDev

Power#

Power

#bs.math:pow {scaling:<scaling>}

Compute $x^y$.

Inputs:

Score $math.pow.base bs.in: The base.

Score $math.pow.exp bs.in: The exponent.

Macro Var scaling [number]: Scalar for the function’s input base and the output.

Outputs:

Return | Score $math.pow bs.out: Result of the operation.

Compute $2.245^6$:

# Once
scoreboard players set $math.pow.base bs.in 2245
scoreboard players set $math.pow.exp bs.in 6
function #bs.math:pow {scale:1000}
tellraw @a [{"text": "(2.245^6)*(1000) = ", "color": "dark_gray"},{"score":{"name":"$math.pow", "objective": "bs.out"}, "color": "gold"}]

Power of 2

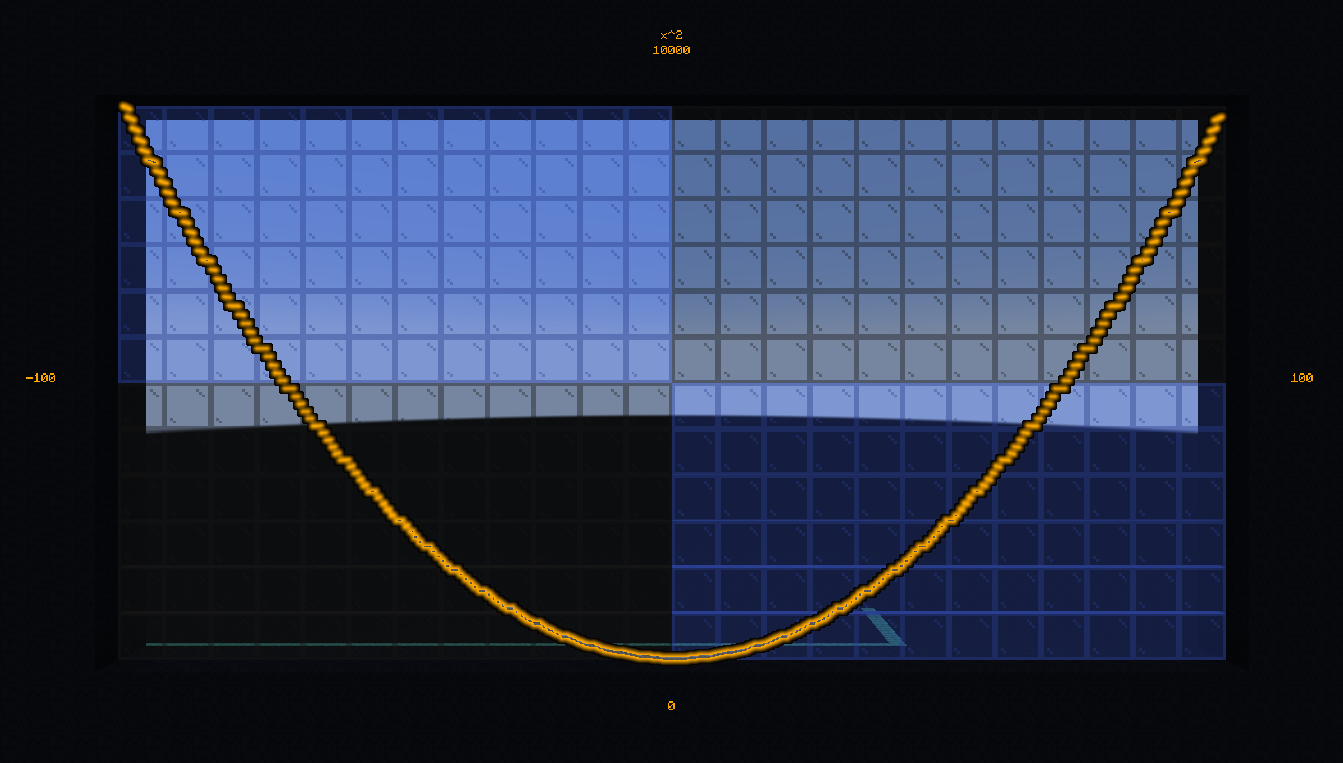
#bs.math:pow2

Compute $2^n$.

Inputs:: Score $math.pow2.exp bs.in: The exponent.
Outputs:: Return | Score $math.pow2 bs.out: Result of the operation.

Compute $2^6$:

# Once
scoreboard players set $math.pow2.exp bs.in 6
function #bs.math:pow2
tellraw @a [{"text": "2^6 = ", "color": "dark_gray"},{"score":{"name":"$math.pow2", "objective": "bs.out"}, "color": "gold"}]

Credits: Aksiome, Leirof

Rounded division#

#bs.math:divide

Divide a number by another then round the result to the nearest integer (Minecraft rounds down to the next integer).

Inputs:

Score $math.divide.num bs.in: The numerator.

Score $math.divide.den bs.in: The denominator.

Outputs:

Return | Score $math.divide bs.out: Result of the division.

Calculate $9/5$:

# Once
scoreboard players set $math.divide.num bs.in 9
scoreboard players set $math.divide.den bs.in 5
function #bs.math:divide
tellraw @a [{"text": "9 / 5 = ", "color": "dark_gray"},{"score":{"name":"$math.divide", "objective": "bs.out"}, "color": "gold"}]

Credits: Aksiome, theogiraudet

Square root#

Integer

#bs.math:isqrt

Compute the square root of an int number.

Inputs:: Score $math.isqrt.value bs.in: Number you want to calculate the square root of.
Outputs:: Return | Score $math.isqrt bs.out: Floored result of the square root.

Calculate and display $\sqrt{42}$:

# Once
scoreboard players set $math.isqrt.value bs.in 42
function #bs.math:isqrt
tellraw @a [{"text": "sqrt(42) = ", "color": "dark_gray"},{"score":{"name":"$math.isqrt", "objective": "bs.out"}, "color": "gold"}]

Decimal

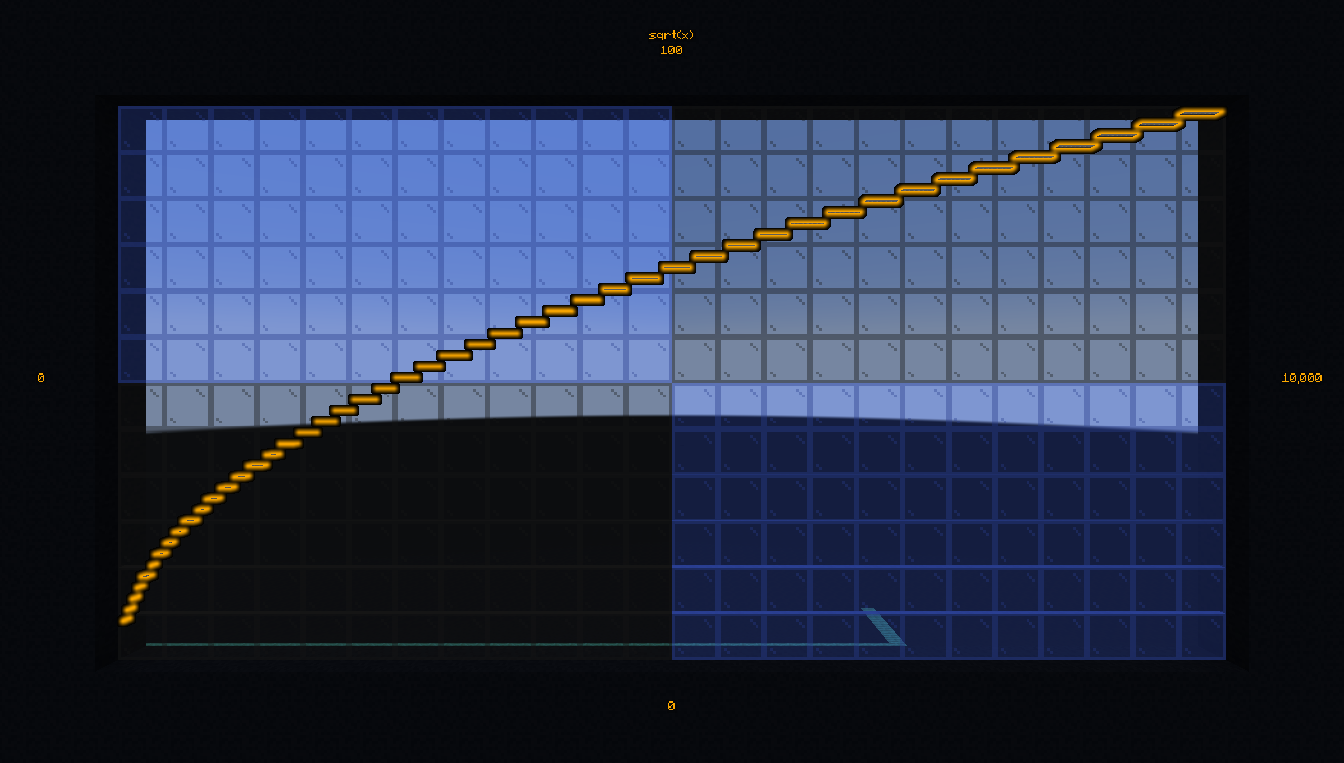
#bs.math:sqrt

Compute the square root of a floating number.

Inputs:: Storage bs:in math.sqrt.value [number]: Number you want to calculate the square root of.
Outputs:: Storage bs:out math.sqrt [float]: Result of the operation.

Calculate and display $\sqrt{42}$:

# Once
data modify storage bs:in math.sqrt.value set value 42
function #bs.math:sqrt
tellraw @a [{"text": "sqrt(42) = ", "color": "dark_gray"},{"nbt": "math.sqrt", "storage": "bs:out", "color": "gold"}]

Credits: Ethanout

Trigonometry#

Cos

#bs.math:cos

Compute the cosine of an angle between 0 and 360.

Inputs:: Score $math.cos.angle bs.in: Angle in degrees shifted by 2 digits (ex: 90.15 -> 9015).
Outputs:: Return | Score $math.cos bs.out: Cosine of the angle shifted by 3 digits (ex: 0.42 -> 420).

Compute and display the cosine of 42:

# Once
scoreboard players set $math.cos.angle bs.in 4200
function #bs.math:cos
tellraw @a [{"text": "cos(42) = ", "color": "dark_gray"},{"score":{"name":"$math.cos", "objective": "bs.out"}, "color": "gold"}]

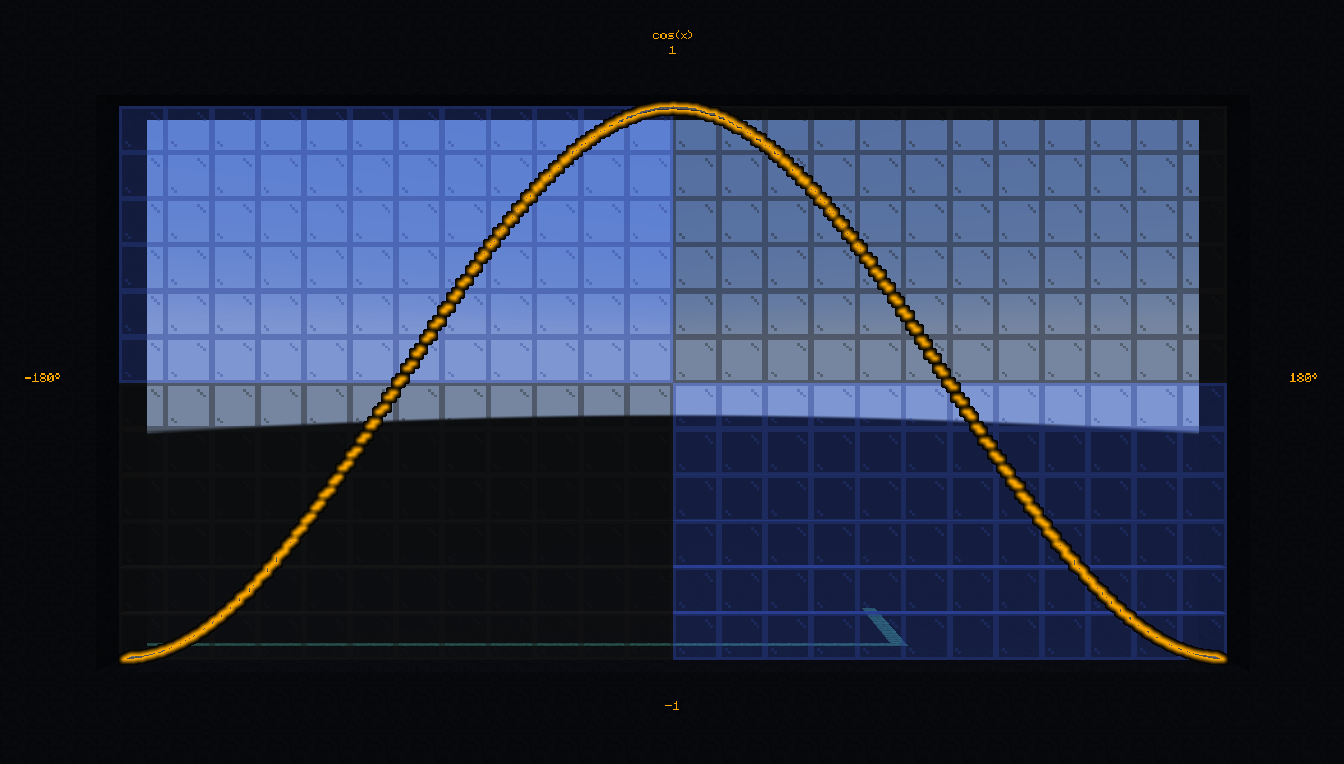
How does it work?

This functions use the Bhaskara approximation which tell us that

\[ \sin(x) \approx \frac{4x(180-x)}{40500-x(180-x)} \quad \forall x \in [0, 180] \]

From this relation, and using the properties

$\sin(-x) = -\sin(x)$ (antisymetry)
$\sin(x+360) = \sin(x)$ (periodicity)

We can compute the sine of any angle and thus the cosine.

Sin

#bs.math:sin

Compute the sine of an angle between 0 and 360.

Inputs:: Score $math.sin.angle bs.in: Angle in degrees shifted by 2 digits (ex: 90.15 -> 9015).
Outputs:: Return | Score $math.sin bs.out: Sine of the angle shifted by 3 digits (ex: 0.42 -> 420).

Compute and display the sine of 42:

# Once
scoreboard players set $math.sin.angle bs.in 4200
function #bs.math:sin
tellraw @a [{"text": "sin(42) = ", "color": "dark_gray"},{"score":{"name":"$math.sin", "objective": "bs.out"}, "color": "gold"}]

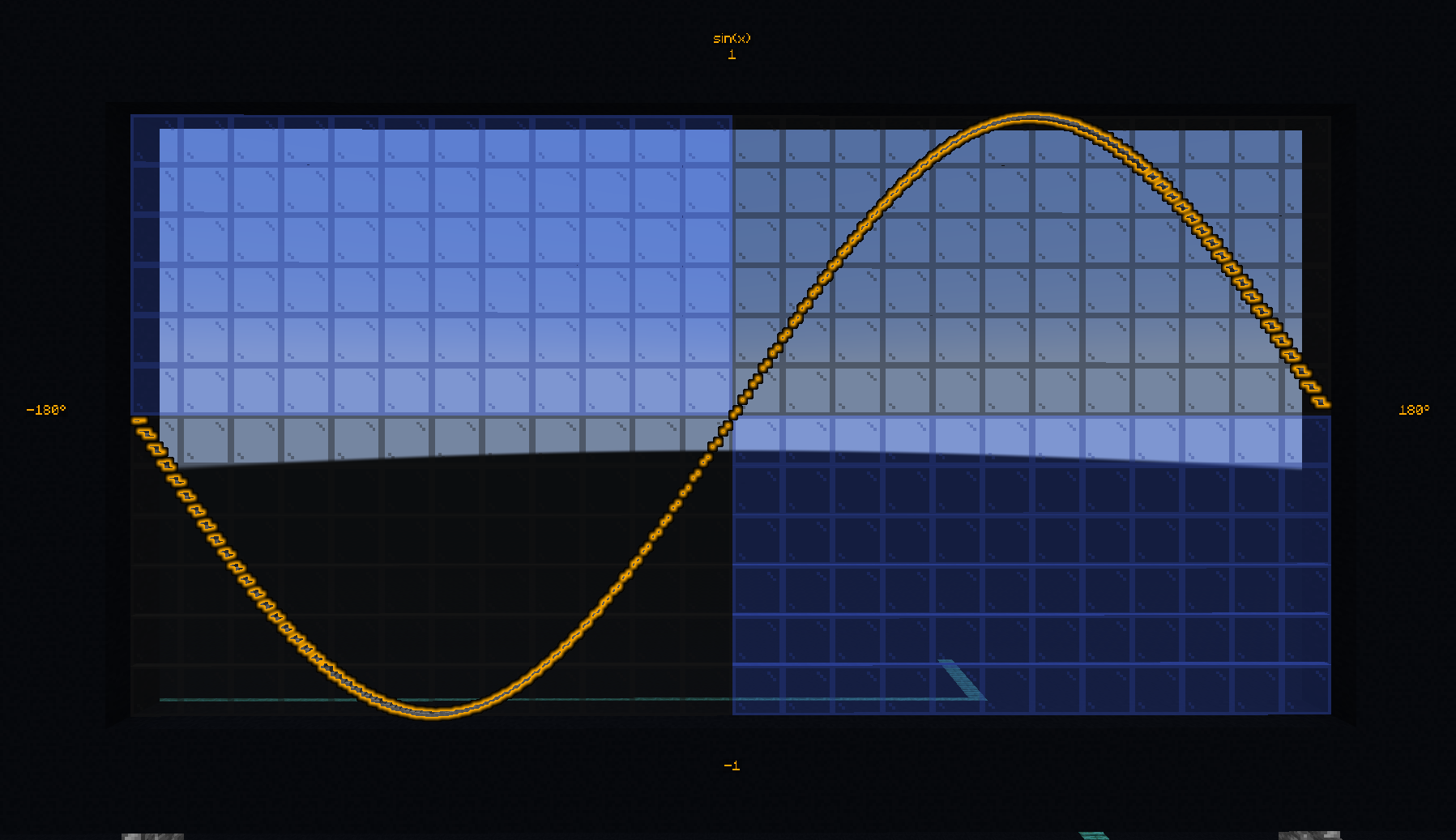
How does it work?

This functions use the Bhaskara approximation which tell us that

\[ \sin(x) \approx \frac{4x(180-x)}{40500-x(180-x)} \quad \forall x \in [0, 180] \]

From this relation, and using the properties

$\sin(-x) = -\sin(x)$ (antisymetry)
$\sin(x+360) = \sin(x)$ (periodicity)

We can compute the sine of any angle.

Tan

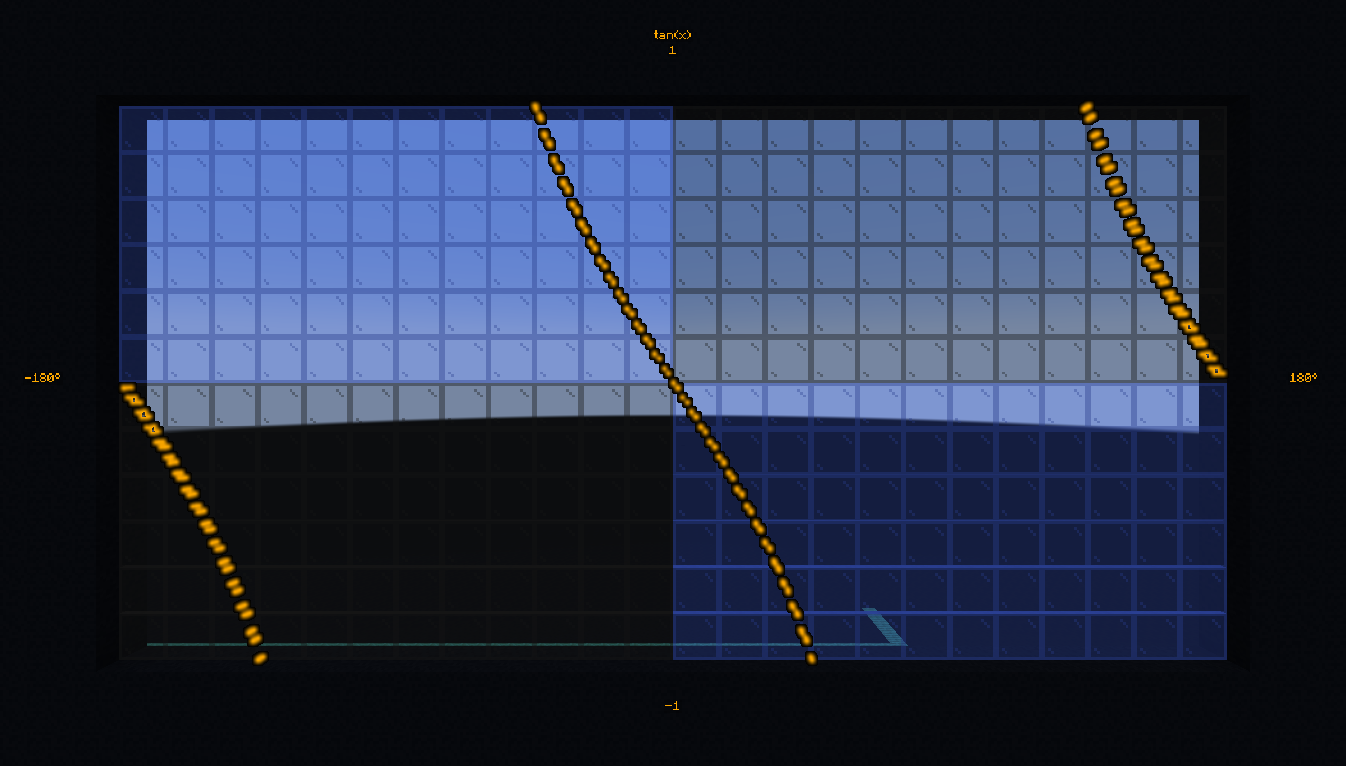
#bs.math:tan

Compute the tangent of an angle between 0 and 360.

Inputs:: Score $math.tan.angle bs.in: Angle in degrees shifted by 2 digits (ex: 90.15 -> 9015).
Outputs:: Return | Score $math.tan bs.out: Tangent of the angle shifted by 3 digits (ex: 0.42 -> 420).

Compute and display the tangent of 42:

# Once
scoreboard players set $math.tan.angle bs.in 4200
function #bs.math:tan
tellraw @a [{"text": "tan(42) = ", "color": "dark_gray"},{"score":{"name":"$math.tan", "objective": "bs.out"}, "color": "gold"}]

Sincos

#bs.math:sincos

Compute both the sine and cosine of an angle between 0 and 360 in a single operation.

Inputs:

Score $math.sincos.angle bs.in: Angle in degrees shifted by 2 digits (ex: 90.15 -> 9015).

Outputs:

Score $math.sincos.cos bs.out: Cosine of the angle shifted by 3 digits (ex: 0.42 -> 420).

Score $math.sincos.sin bs.out: Sine of the angle shifted by 3 digits (ex: 0.42 -> 420).

Compute and display the sine and cosine of 42:

# Once
scoreboard players set $math.sincos.angle bs.in 4200
function #bs.math:sincos
tellraw @a [{"text": "cos(42) = ", "color": "dark_gray"},{"score":{"name":"$math.sincos.cos", "objective": "bs.out"}, "color": "gold"}]
tellraw @a [{"text": "sin(42) = ", "color": "dark_gray"},{"score":{"name":"$math.sincos.sin", "objective": "bs.out"}, "color": "gold"}]

Credits: Aksiome, Leirof

💬 Did it help you?

Feel free to leave your questions and feedbacks below!