🧮 Math#

bs.math:_

The beatifull world of mathematics… in Minecraft!

“Mathematics has very subtle inventions that can be of great service, both to satisfy the curious and to facilitate all arts and reduce the labor of men.”

—René Descartes

Algebra#

bs.math:algebra/_

This folder allows you to perform algebra operations

Basis rotation 3D#

bs.math:algebra/basis_rotation_3d

Allows to obtain the equivalent of the vector passed in parameter in a base with a different orientation. Useful to convert an absolute/relative position into a local position for a given entity.

Inputs

(execution) as <entities>: The entities you want to perform the computation on
(scores) @s bs.in.[0,1,2]: Vector coordinates \((X,Y,Z)\) in the starting base
(scores) @s bs.in.[3,4]: Horizontal (along \(\hat{z}\)) and vertical (along \(\hat{\phi}\)) rotation (in degree) from the starting base

Outputs

(scores) bs.out.[0,1,2]: Vector coordinates \((X',Y',Z')\) in the target base

Examples

A block is in ~2 ~5 ~10 from me, I want to have this position in local coordinate (^? ^? ^?)

# One time

# Relative coordinates (we multiply by 1000 to have more precision on the result, which will also be multiplied by 1000)
scoreboard players set @s bs.in.0 2000
scoreboard players set @s bs.in.1 5000
scoreboard players set @s bs.in.2 10000

# Difference between my orientation (= that of the coondata grid ^X ^Y ^Z) and the orientation of the Minecraft blocks grid (~X ~Y ~Z)
function bs.orientation:get
scoreboard players operation @s bs.in.3 = @s bs.ori.h
scoreboard players operation @s bs.in.4 = @s bs.ori.v

# Perform the basic rotation
function bs.math:algebra/basis_rotation_3d

# See the result
tellraw @a [{"text": "X = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"},{"text":", Y = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs. res1"},"color":"gold"},{"text":", Z = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.2"},"color":"gold"}]

I want to have a vector pointing to where I’m looking, but in relative coordinates ~X ~Y ~Z (also called “classical” vector in this library)

# Once

# Retrieve a vector ^ ^ ^1 corresponding to a vector directed according to the orientation of the entity (we multiply by 1000 to have more precision on the result, which will also be multiplied by 1000)
scoreboard players set @s bs.in.0 0
scoreboard players set @s bs.in.1 0
scoreboard players set @s bs.in.2 1000

# Get the orientation
function bs.orientation:get
scoreboard players operation @s bs.in.3 = @s bs.ori.h
scoreboard players operation @s bs.in.4 = @s bs.ori.v

# Reversal of the orientation since we want to have the relative orientation of the game grid compared to the orientation of the player (unlike the previous example)
scoreboard players operation @s bs.in.3 *= -1 bs.const
scoreboard players operation @s bs.in.4 *= -1 bs.const

# Perform the basic rotation
function bs.math:algebra/basis_rotation_3d

# See the result
tellraw @a [{"text": "X = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"},{"text":", Y = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs. res1"},"color":"gold"},{"text":", Z = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.2"},"color":"gold"}]

Common#

bs.math:common/_

This folder contains the usual math functions

Rounded division#

bs.math:common/divide

Allows you to divide one number by another by rounding the result to the nearest whole number (where Minecraft rounds down to the next whole number).

Inputs

(execution) as <entities>: The entities you want to perform the operation on
(score) @s bs.in.0: The numerator
(score) @s bs.in.1: The denominator

Output

(score) @s bs.out.0: The result of the division

Example

Calculate \(9/5\)

# Once
scoreboard players set @s bs.in.0 9
scoreboard players set @s bs.in.1 5
function bs.math:common/divide
tellraw @a [{"text": "9 / 5 = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"}]

Exponential#

bs.math:common/exp

Compute the exponential of the number passed in parameter on the score bs.in.0 and return the result on the score bs.out.0

Inputs

(execution) as <entities>: The entities you want to perform the operation on
(score) @s bs.in.0: The number to be exponentiated shifted by two digits (1,2345 -> 123) for better precision in integer scores

Technical limitation

Due to the limit of integers that can be stored in a score, the interval of bs.in.0 is limited to [-600,1200] (i.e. [-6;12] in real value)

Output

(score) @s bs.out.0: The result of the operation shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Example

Calculate \(exp(3)\)

# Once
scoreboard players set @s bs.in.0 300
function bs.math:common/exp
tellraw @a [{"text":"exp(3)*10^3 = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.0"},"color":"gold"}]

Note

We are looking for a better implementation of this function. If you have any ideas, please join our Discord server to discuss with us!

Factorial#

bs.math:common/factorial

Compute the factorial of the number

Inputs

(execution) as <entities>: The entities you want to perform the operation on
(score) @s bs.in.0: The number to be factorialized

Technical limitation

Due to the limit of integers that can be stored in a score, the interval of bs.in.0 is limited to [0,12]

Output

(score) @s bs.out.0: The result of the operation

Example

Compute \(3!\)

# Once
scoreboard players set @s bs.in.0 3
function bs.math:common/factorial
tellraw @a [{"text": "3! = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.0"},"color":"gold"}]

Greatest common denominator#

bs.math:common/gcd

Compute the greatest common denominator of two numbers

Inputs

(execution) as <entities>: The entities you want to perform the operation on
(score) @s bs.in.0: The first number
(score) @s bs.in.1: The second number

Output

(score) @s bs.out.0: The greatest common denominator

Example

Calculate the greatest common denominator between 16 and 12

# Once
scoreboard players set @s bs.in.0 16
scoreboard players set @s bs.in.1 12
function bs.math:common/gcd
tellraw @a [{"text": "gcd(16,12) = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"}]

Logarithm#

Base e (Neperian)

bs.math:common/log

Compute the Neperian logarithm (base e) of a number

Inputs

(execution) as <entities>: The entities you want to perform the operation on
(score) @s bs.in.0: The number to be logarithmized, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Output

(score) @s bs.out.0: The result of the operation, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Example

Calculate \(ln(28)\)

# Once
scoreboard players set @s bs.in.0 28000
function bs.math:common/log
tellraw @a [{"text":"ln(28)*10^3 = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.0"},"color":"gold"}]

Base 2

bs.math:common/log2

Compute the logarithm in base 2 of a number

Inputs

(execution) as <entities>: The entities you want to perform the operation on
(score) @s bs.in.0: The number to be logarithmized, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Output

(score) @s bs.out.0: The result of the operation, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Example

Calculate \(log_2(28)\):

# Once
scoreboard players set @s bs.in.0 28000
function bs.math:common/log2
tellraw @a [{"text":"log2(28)*10^3 = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.0"},"color":"gold"}]

Base 10

bs.math:common/log10

Compute the logarithm in base 10 of a number

Inputs

(execution) as <entities>: The entities you want to perform the operation on
(score) @s bs.in.0: The number to be logarithmized, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Output

(score) @s bs.out.0: The result of the operation, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Example

Calculate \(log_{10}(28)\)

# Once
scoreboard players set @s bs.in.0 28000
function bs.math:common/log10
tellraw @a [{"text":"log10(28)*10^3 = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.0"},"color":"gold"}]

Base a

bs.math:common/loga

Computes the logarithm in base a of a number

Inputs

(execution) as <entities>: The entities you want to perform the operation on
(score) @s bs.in.0: The number to be logarithmized, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores
(score) @s bs.in.1: The base of the logarithm (not shifted)

Output

(score) @s bs.out.0: The result of the operation, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Example

Calculate \(log_4(28)\)

# Once
scoreboard players set @s bs.in.0 28000
scoreboard players set @s bs.in.1 4
function bs.math:common/loga
tellraw @a [{"text":"log4(28)*10^3 = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.0"},"color":"gold"}]

Power#

Normal

bs.math:common/pow

Compute \(x^y\)

Inputs

(execution) as <entities>: The entities you want to perform the calculation on
(score) @s bs.in.0: The base
(score) @s bs.in.1: The exponent

Output

(score) @s bs.out.0: The result of the calculation

Example

Compute \(2^6\)

# Once
scoreboard players set @s bs.in.0 2
scoreboard players set @s bs.in.1 6
function bs.math:common/pow
tellraw @a [{"text": "2^6 = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"}]

Scale 3

bs.math:common/pow/scale/3

Compute \(x^y\)

Inputs

(execution) as <entities>: The entities you want to perform the calculation on
(score) @s bs.in.0: The base, a number shifted by 3 digits (1,2345 -> 1234)
(score) @s bs.in.1: The exponent, not shifted

Output

(score) @s bs.out.0: The result of the calculation, a number shifted by 3 digits (1,2345 -> 1234)

Example

Compute \(2.345^6\)

# Once
scoreboard players set @s bs.in.0 2345
scoreboard players set @s bs.in.1 6
function bs.math:common/pow/scale/3
tellraw @a [{"text": "2.345^6 = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"}]

Square root#

bs.math:common/sqrt

Compute the square root of the number

Inputs

(execution) as <entities>: The entities you want to perform the calculation on
(score) @s bs.in.0: The number you want to calculate the square root of

Output

(score) @s bs.out.0: The result of the calculation

Example

Calculate and display \(\sqrt{42}\)

# Once
scoreboard players set @s bs.in.0 42
function bs.math:common/sqrt
tellraw @a [{"text": "sqrt(42) = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"}]

How does it work?

This system rely on a very simple mathematical concept called dichotomy. As the maximum number that a score can handle is \(2^{31}-1 = 2,147,483,647\), the maximum square root is \(\sqrt{2,147,483,647} \approx 46,340\). Also, we are dealing with only integer number, so we have a finite number of possible square root. The idea is then to take a number at half of the maximum limit and compute the square of this number. If it is upper thant the input, then we decrease our selected number by a quarter of the maximum limit (and if it’s lower, we increase it). We do this operation again and again by increasing/decreasing with \(2^N\) time the maximum numer (\(N\) being the number of iterations) until finding the square root.

As this algorithm converge using a \(2^N\) iterator, the convergeance occure in \(N=\log_2(\text{max limit}) = log_2(46,340) \approx 16\) iterations.

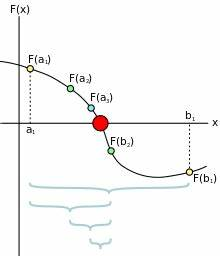
For a conveniant reason, instead of taking half of the maximum limite, we take the first power of two that is above. In this way, every division by \(2^N\) lead to an integer number.

Special#

bs.math:special/_

This folder contains functions that are of special interest in algortihms (but not or not much in formal mathematics)

Retrieve the next power of 2#

bs.math:special/get_next_pow2

Compute the power of 2 directly superior to the number given in parameter.

Inputs

(execution) as <entities>: The entities you want to perform the calculation on
(score) @s bs.in.0: The number from which you want to calculate the next power of 2

Output

(score) @s bs.out.0: The result of the calculation

Example

Find the power of 2 greater than 43

# Once
scoreboard players set @s bs.in.0 43
function bs.math:special/get_next_pow2
tellraw @a [{"text":"get_next_pow2(43) = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.0"},"color":"gold"}]

Random number generator#

bs.math:special/random

Generates a random number

Inputs

(execution) as <entities>: The entities you want to perform the calculation on

Output

(score) @s bs.out.0: An integer random number between \(-2^{31}\) and \(2^{31}-1\)

Tip

To reduce this interval, execute the function then do a “modulo” operation on the result (random % 10 -> the random number will be included in the interval [0;9])

Example

Get and display a random number between 0 and 100:

# Once
function bs.math:special/random
scoreboard players operation @s bs.out.0 %= 101 bs.const
tellraw @a [{"text": "random() = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"}]

Beware: the score `bs.const` does not contain all possible
values. Make sure the value you want to use exists and initialize it
if necessary.

Trigonometry#

bs.math:trig/_

This folder contains basic trigonometry functions, opening a lot of doors to creative possibilities in Minecraft.

Arccosine#

bs.math:trgi/arccos

Calculate the arccosinus of a value between -1 and 1

Inputs

(execution) as <entities>: The entities you want to perform the calculation on
(score) @s bs.in.0: The value you want to calculate the arccosine of, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Output

(score) @s bs.out.0: The result of the calculation, in degrees (not shifted)

Example

Calculate and display the arccos of 0,42

# Once
scoreboard players set @s bs.in.0 420
function bs.math:trig/arccos
tellraw @a [{"text":"arccos(0.42) = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.0"},"color":"gold"}]

Arcsine#

bs.math:trg/arcsin

Compute the arcsinus of a value between -1 and 1

Inputs

(execution) as <entities>: The entities you want to perform the calculation on
(score) @s bs.in.0: The value you want to calculate the arcsine of, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Output

(score) @s bs.out.0: The result of the calculation, in degrees (not shifted)

Example

Calculate and display the arcsinus of 0.42

# Once
scoreboard players set @s bs.in.0 420
function bs.math:trig/arcsin
tellraw @a [{"text":"arcsin(0.42) = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.0"},"color":"gold"}]

Arctangent#

bs.math:trig/arctan

Compute the arctangent of a value between -infinite and +infinite

Inputs

(execution) as <entities>: The entities you want to perform the calculation on
(score) @s bs.in.0: The value you want to calculate the arctangent of, shifted by 3 digits (1,2345 -> 1234) for better precision in integer scores

Output

(score) @s bs.out.0: The result of the calculation, in degrees (not shifted)

Example

Calculate and display the arctan of 0.42

# Once
scoreboard players set @s bs.in.0 420
function bs.math:trig/arctan
tellraw @a [{"text":"arctan(0.42) = ","color":"dark_gray"},{"score":{"name":"@s","objective":"bs.out.0"},"color":"gold"}]

How does it work?

This function use two approximations to calculate the arctangent of a value:

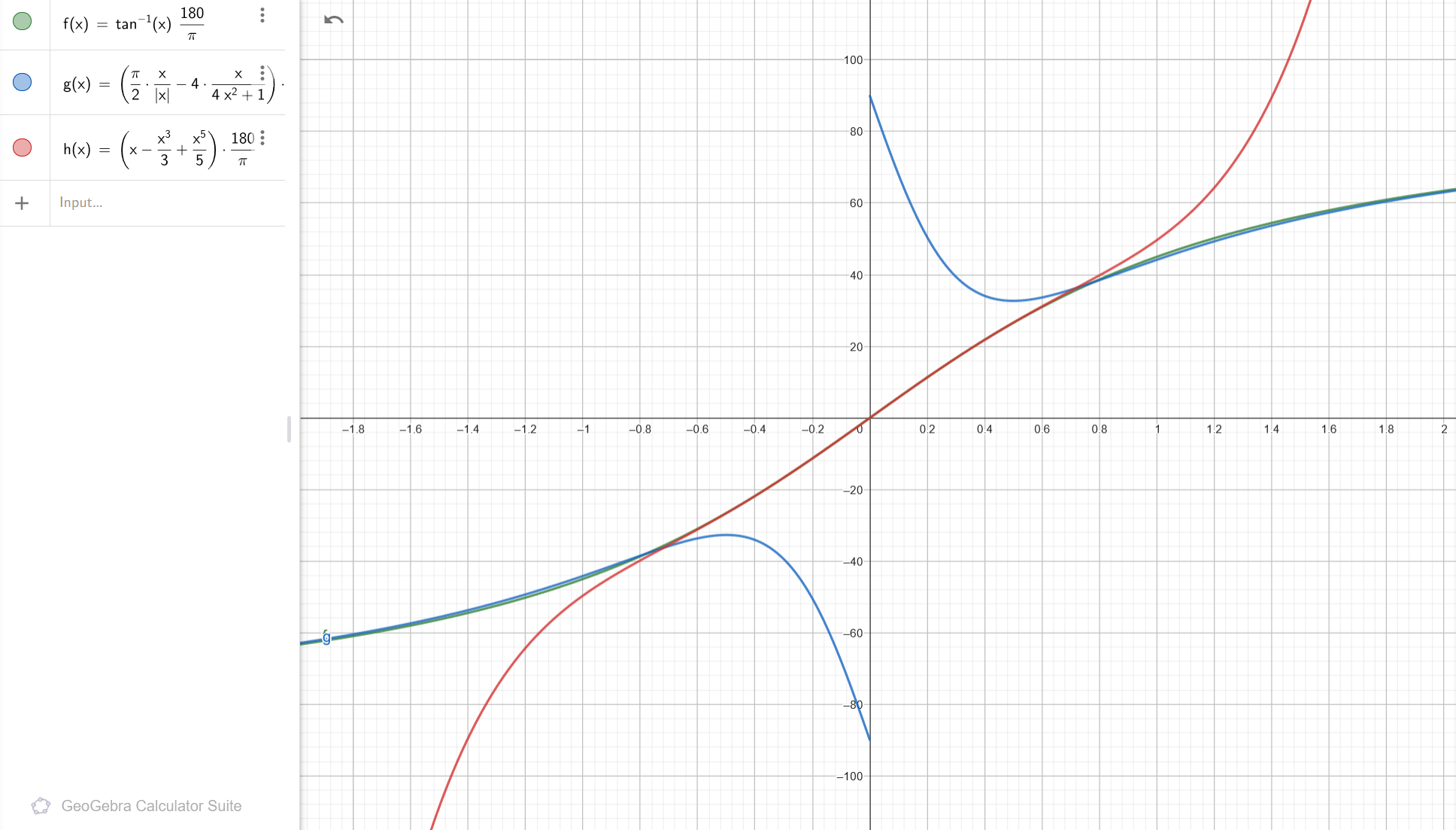
\[\begin{split} \begin{cases} \tan(x) = \left(\frac \pi 2 \frac x {|x|} - 4 \frac x {4x^2 + 1}\right)\frac \pi {180} &\forall |x| \geq 0.72\\ \tan(x) = \left( x - \frac {x^3} 3 + \frac {x^5} 5 \right)\frac \pi {180} & \forall |x| < 0.72 \end{cases} \end{split}\]

Cosine#

bs.math:trig/cos

Compute the cosine of an angle between 0 and 360

Inputs

(execution) as <entities>: The entities you want to perform the calculation on (score) @s bs.in.0; The angle in degrees

Outputs

(score) @s bs.out.0: The cosine of the angle shifted by 3 digits (ex: 0.42 -> 420)

Example

Calculate and display the cosine of 42

# Once
scoreboard players set @s bs.in.0 42
function bs.math:trig/cos
tellraw @a [{"text": "cos(42) = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"}]

How does it work?

This function use the property \(cos(x) = sin(x + 90)\) to compute the cosine of an angle. It then uses the sine function to compute the result.

Sine#

bs.math:trig/sin

Computes the sine of an angle between 0 and 360

Inputs

(execution) as <entities>: The entities you want to perform the calculation on (score) @s bs.in.0; The angle in degrees

Outputs

(score) @s bs.out.0: The sine of the angle shifted by 3 digits (ex: 0.42 -> 420)

Example

Calculate and display the sine of 42

# Once
scoreboard players set @s bs.in.0 42
function bs.math:trig/sin
tellraw @a [{"text": "sin(42) = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"}]

How does it work?

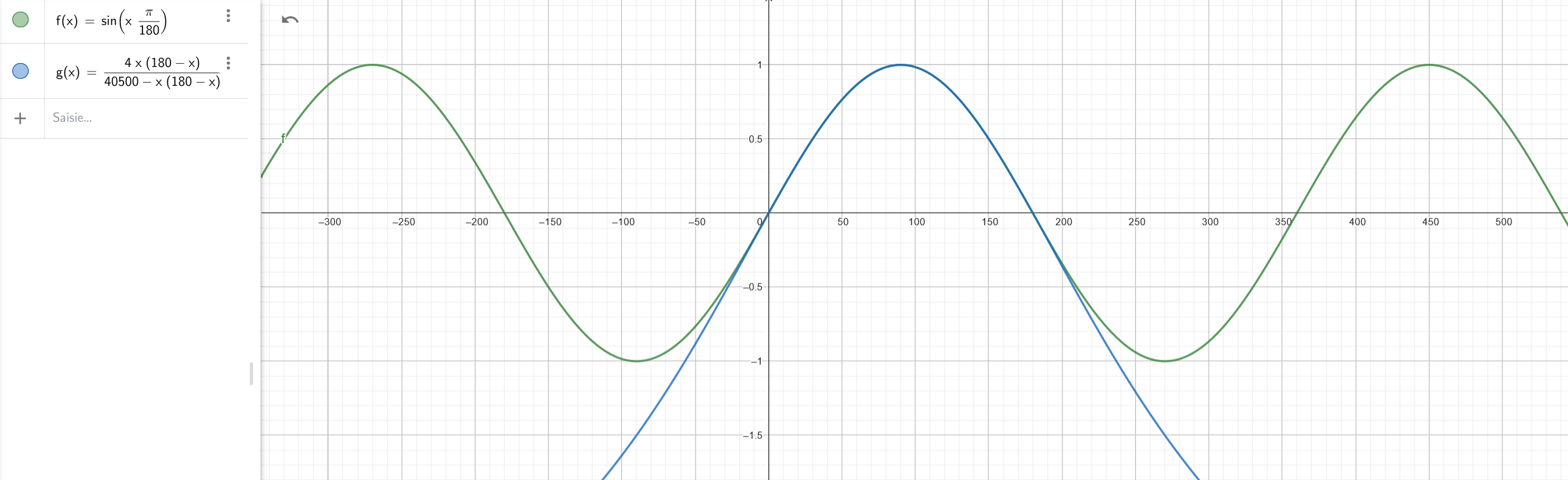
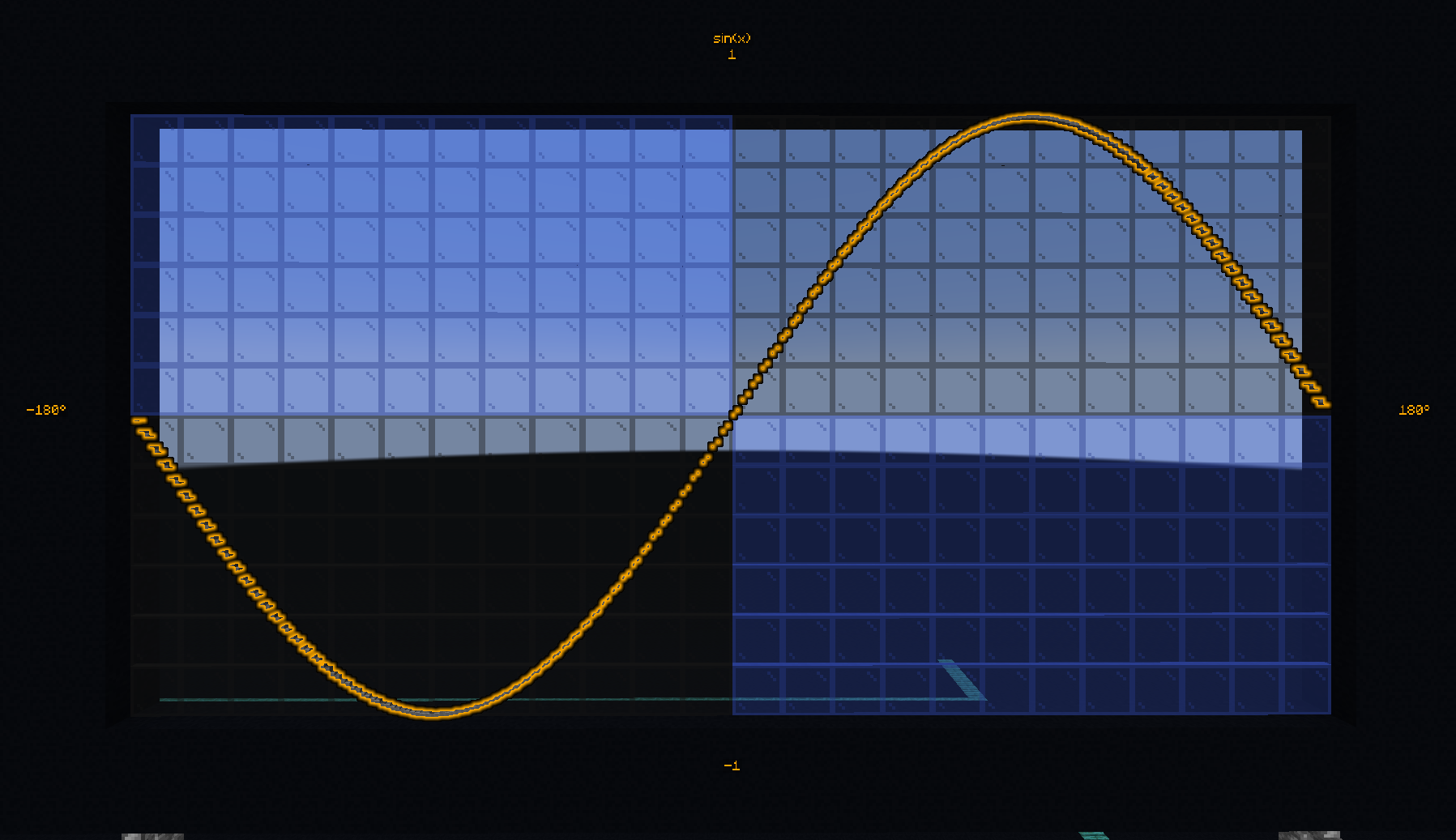
This function use the Bhaskara approximation which tell us that

\[ \sin(x) \approx \frac{4x(180-x)}{40500-x(180-x)} \quad \forall x \in [0, 180] \]

From this relation, and using the properties

\(\sin(-x) = -\sin(x)\) (antisymetry)
\(\sin(x+360) = \sin(x)\) (periodicity)

We can compute the sine of any angle.

Tangent#

bs.math:trig/tan

Compute the tangeant of an angle between 0 and 360

Inputs

(execution) as <entities>: The entities you want to perform the calculation on
(score) @s bs.in.0: The angle in degrees (not shifted)

Outputs

(score) @s bs.out.0: The tangeant of the angle shifted by 3 digits (ex: 0.42 -> 420)

Example

Calculate and display the tengeante of 42

# Once
scoreboard players set @s bs.in.0 42
function bs.math:trig/tan
tellraw @a [{"text": "tan(42) = ", "color": "dark_gray"},{"score":{"name":"@s", "objective": "bs.out.0"}, "color": "gold"}]

💬 Did it help you?

Feel free to leave your questions and feedbacks below!

Bookshelf documentation

🧮 Math

Contents

🧮 Math#

Algebra#

Basis rotation 3D#

Common#

Rounded division#

Exponential#

Factorial#

Greatest common denominator#

Logarithm#

Power#

Square root#

Special#

Retrieve the next power of 2#

Random number generator#

Trigonometry#

Arccosine#

Arcsine#

Arctangent#

Cosine#

Sine#

Tangent#